Исследование эффективности и температурной устойчивости чирпированного кристалла PPLN в эксперименте по удвоению частоты на длине волны 1064 нм - 02

2. Теоретический анализ

2.1 Температурная устойчивость

Под температурной устойчивостью понимается стабильность кристалла с удвоенной частотой по отношению к температуре. В частности, когда температура колеблется, мощность света с удвоенной частотой не сильно пострадает. Влияние температуры на процесс удвоения частоты происходит главным образом за счет влияния на фазовую расстройку. Во время процесса удвоения частоты, в случае аппроксимации малого сигнала, мощность света с удвоенной частотой может быть выражена как:

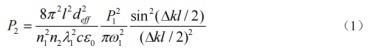
Вуравнение 1,л– длина кристалла удвоения частоты;д_эфф– эффективный нелинейный коэффициент;с– скорость света в вакууме;ε₀– диэлектрическая проницаемость вакуума;п_я,λ_я,н_я, иω_яявляютсятмощность, длина волны, показатель преломления и радиус перетяжки лучажфундаментальная частоталучи частота-сомневатьсявеллучсоответственно. Тон подписываетя=1, 2 соответствуют основной частотелучи удвоенная частоталучсоответственно; величина фазового рассогласования Δк"="к₂-2к₁,в какой волне vЭкторк_я"="(н_я2π)/λ_я. Это видно из уравнения1, что только при выполнении условия синхронизма, т. е. когда ∆к=0, можно получить максимальную оптическую мощность с удвоением частоты. В процессе квазисинхронизма, поскольку направление спонтанной поляризации нелинейного кристалла искусственно и периодически изменяется, период поляризацииΛвведем вектор обратной решеткиг_м. Связь между вектором обратной решетки и периодом поляризации:

г_м"="м(2π/Λ) (2)

Втздесьмпредставляет собойчисломзаказать квазисинхронизм.Затемрассогласование фаз в процессе удвоения частоты можно переписать как:

Δк'"="к₂-2к₁-г_м(3)

Это известно изСуравнение Элмейера:шПри изменении температуры показатель преломлениян_ятакже будет затронуто, что, в свою очередь, повлияет на фазовую расстройку Δк. Поскольку период поляризации PPLN(www.wisoptic.com)представляет собой один период, а введенный обратный вектор представляет собой фиксированное значение, фазовый синхронизм Δк'= 0 может быть достигнуто только при определенных длинах волн и определенных температурных условиях.Поэтомумы можем знать, что ключевым моментом для достижения температурной устойчивости является расширение полосы усиления поляризованного кристалла, чтобы вектор обратной решетки мог охватывать определенный диапазон.ифазовое рассогласование все еще может удовлетворять Δк'= 0 при изменении температуры.яДругими словами, температурная устойчивость связана с шириной полосы усиления кристалла. Чем больше полоса усиления, тем лучше температурная устойчивость кристалла. Период поляризации PPLN можно выразить как функцию положенияследующее:

В формулеД_г- степень чирпа кристалла CPPLN(www.wisoptic.com), иΛ₀– начальный период CPPLN. Это видно изЭуравнение 4, что период поляризации CPPLN охватываетΛ₁= 2πΛ₀иΛ₂"="Λ₀/[(1+Д_гΛ₀л)/2π]. И она меняется непрерывно в этом диапазоне, то есть CPPLN этой структуры может обеспечить вектор обратной решетки, который непрерывно меняется в определенном диапазоне. Когда фазовое рассогласование k изменяется в этом диапазоне из-за температуры, вектор обратной решетки CPPLN прекрасно компенсирует его изменяющееся значение, чтобы гарантироватьΔк' = 0, то есть эффективность преобразования света с удвоенной частотой может поддерживаться на очень высоком уровне в определенном температурном диапазоне. Однако следует отметить, что чем больше диапазон периодов поляризации CPPLN, тем не лучше, поскольку увеличение чирпа приведет к уменьшению эффективного коэффициента нелинейности. Поэтому в реальном производственном процессе необходимо обеспечить баланс между температурной устойчивостью и максимальной эффективностью умножения частоты.