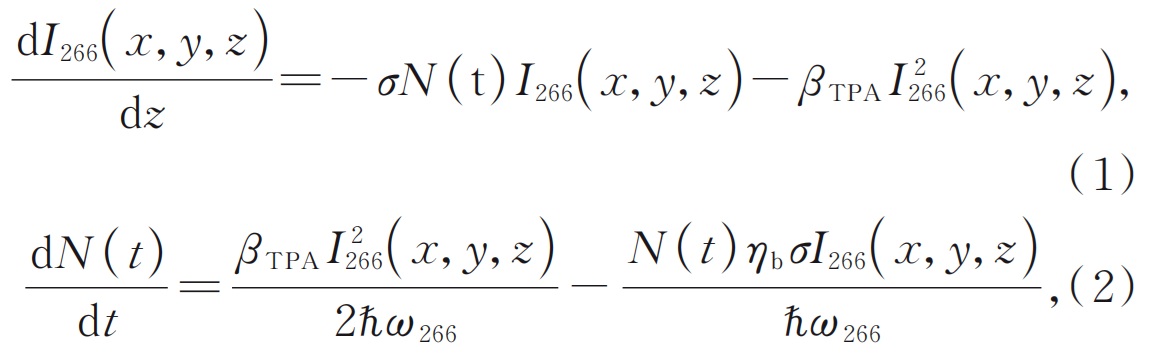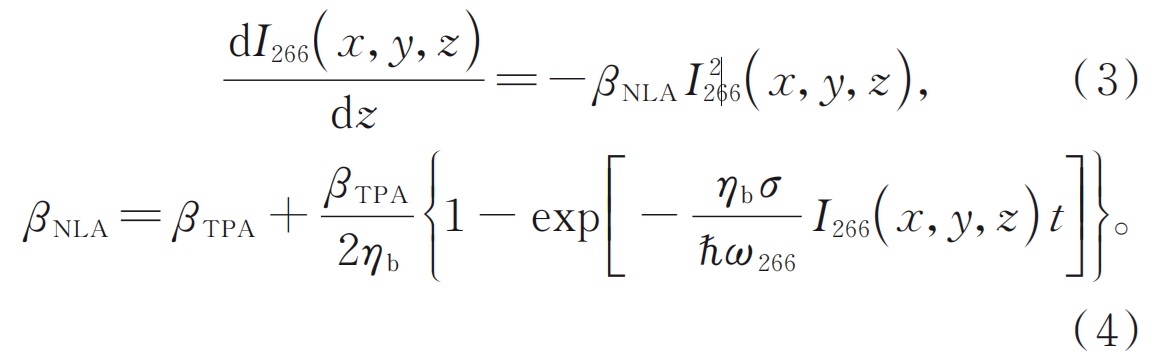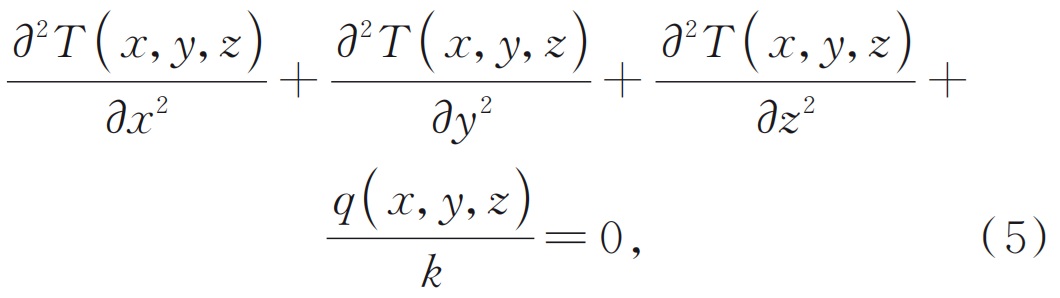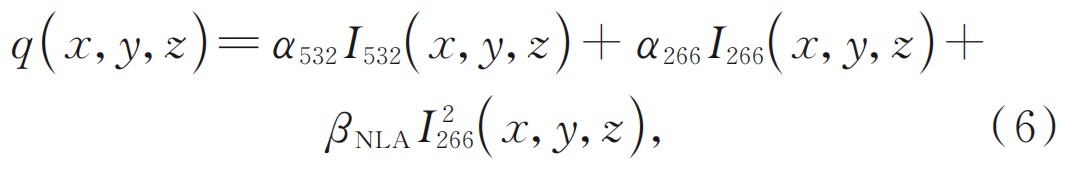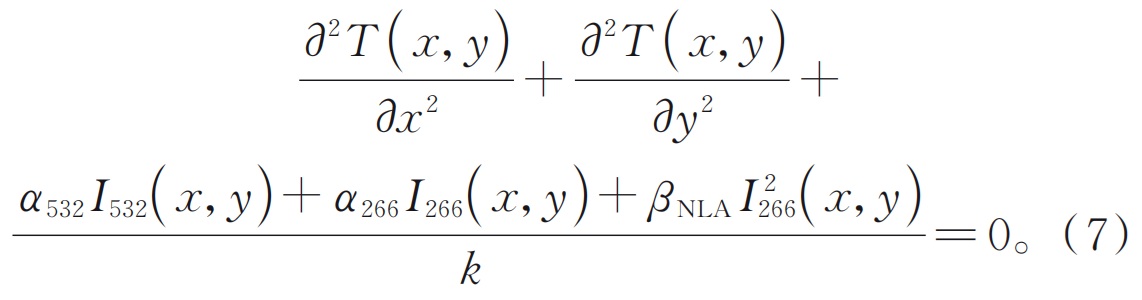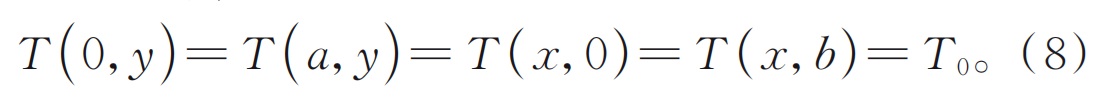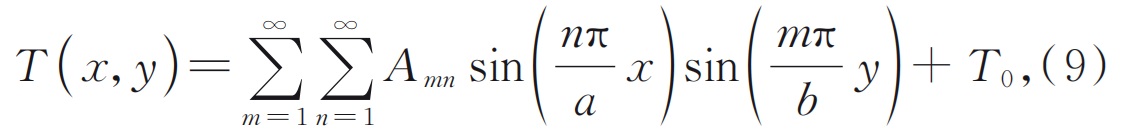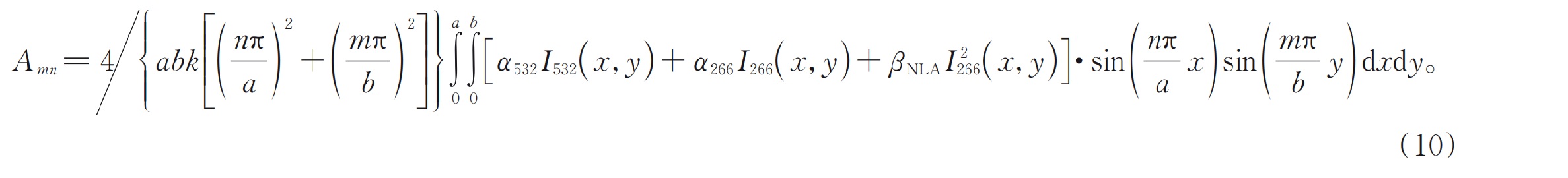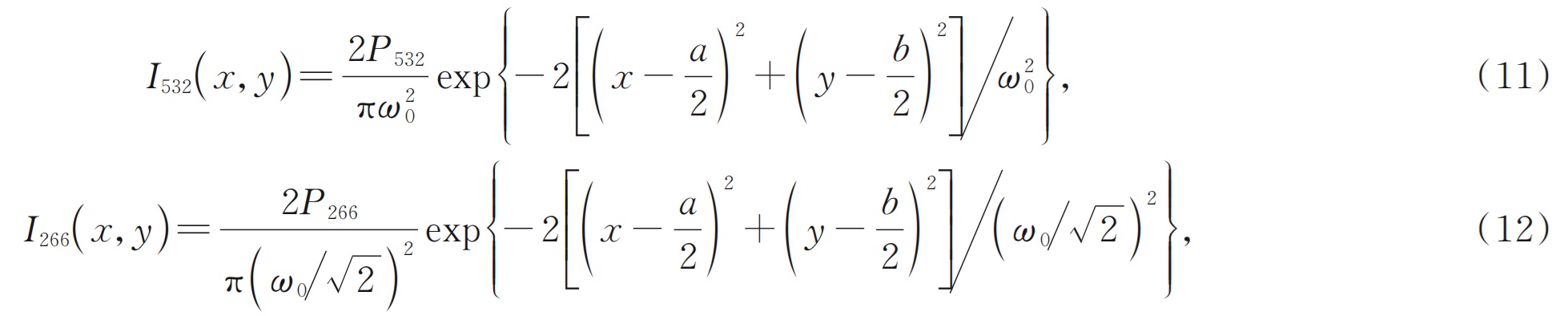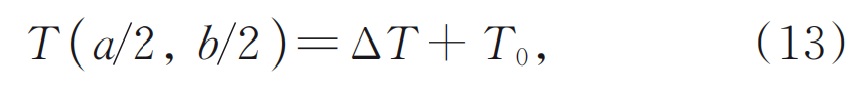Исследование термических характеристик 266 нм глубиной ультрафиолетовой лазер, генерируемой кристаллом BBO - 05

04 Теоретическое исследование тепловых свойств

Приведенный выше эксперимент показывает, что кристалл BBO(www.wisoptic.com)генерирует серьезную тепло в процессе четырехлетней четырехлетней четырехлетней. Известно, что разрыв в полосе энергии в кристалле BBO составляет 6,56 эВ, в то время как единственная энергия фотона 266 нм и 532 нм лазеры составляет 4,66 эВ и 2,33 эВ соответственно. Теоретически, кристалл не имеет единого фотонного поглощения 266 нм и 532 нм лазеров. Только потому, что небольшое количество примесей, содержащихся в кристалле, будет вводить новую структуру уровня энергии и приведет к более слабым линейному поглощению, доминирующим фактором, вызывающим тепло, в кристалле является двухфотонное поглощение лазера 266 нм. При рассмотрении двухфотонного поглощения 266 нм лазера BBO кристаллом BBO в процессе четырехлетней четырехлетней четырехлетней части, предполагается, что абсорбция с двумя фотоном приведет к образованию динамических дефектов центра цветовых центров в кристалле. Уравнения, контролирующие интенсивность ультрафиолетового света и плотность цветовых центров:

Где:я₂₆₆(x, y, z) - это распределение плотности мощности 266 нм;β_TPAявляется двухфотонным коэффициентом поглощения кристалла BBO для лазера 266 нм;ω₂₆₆является угловой частотой лазерных фотонов 266 нм;σявляется поперечное сечение поглощения дефекта в цвете;η_{беременный}Является ли эффективность отбеливания дефекта цвета;Не(Т)-это зависимая от времени плотность Центрального центра. КогдаТ= 0,Не(Т) = 0, поэтому мы можем получить:

При определенной мощности ультрафиолетового ультрафиолета серия нелинейных поглощения поглощения, вызванных поглощением двухфотонных и дефектов Цветового центра, создаваемых им внутри BBO(www.wisoptic.com)хрусталможет быть измерен с помощью нелинейного коэффициента поглощенияβ_Нла, чье выражение показано в формуле (4). Когда кристалл BBO генерирует тепло из-за нелинейного поглощения, относительно стабильное распределение поля температуры будет сформировано внутри кристалла в фиксированных условиях контроля внешней температуры, что подчиняется уравненному уравнению теплопроводности устойчивого состояния:

Где:Т(x, y, z) - это распределение температуры внутри кристалла;kявляется теплопроводности, предполагая, что коэффициент является изотропным внутри кристалла, среднее значение теплопроводности в направлениях, перпендикулярных и параллельно оптической оси;Q.(x, y, z) представляет тепло, генерируемое источником тепла на единицу объема на единицу времени внутри кристалла. Принимая во внимание нелинейное поглощение кристалла в лазер 266 нм, небольшое количество линейного поглощения кристалла также учитывается 266 нм и 532 нм лазеров. Его выражение:

Где:α₅₃₂иα₂₆₆являются линейными коэффициентами поглощения кристалла BBO для лазеров 532 нм и 266 нм соответственно;_я532(x, y, z) - это распределение плотности мощности 532 нм лазер. Поскольку четырехкратный частотный кристалл короче, плотность мощности зеленого света и ультрафиолетового света в продольном направлении кристалла не сильно меняется, и температуру кристаллической стороны контролируется, поэтому изменение температуры в продольном направлении кристалла может быть проигнорирована. Формула (5) может быть выражена как:

Предполагая, что площадь поперечного сечения кристалла BBO (а×беременный) мм², сторона кристалла сохраняется при постоянной температуреТ₀с помощью нагревательного устройства, и прямоугольная система координат построена с любой вершиной кристалла в качестве источника. Во время процесса теплопроводности кристалла BBO он следует за первым типом граничных условий, затем:

Когда инцидент 532 нм зеленый свет и сгенерированный ультрафиолетовый лазер 266 нм распространяются вдоль центра кристалла, в соответствии с граничными условиями может быть дано общее решение поля температуры кристалла, состоящее из двух собственных функций:

Где:А_мнженнеизвестный коэффициент. Заменить уравнение (9) в уравнение теплопроводности (7) и, используя ортогональность тригонометрических функций, мы можем получить выражение неизвестного коэффициента:

Предполагая, что зеленый свет и ультрафиолетовый лазер оба являются ПЭМ₀₀Режим гауссовых лучей, выражение их распределения интенсивности света составляет:

ГдеП₅₃₂иП₂₆₆силы зеленого света и ультрафиолетового света соответственно;ω₀Радиус талии зеленого света в кристалле BBO(www.wisoptic.com)Полем Поскольку зеленый свет и ультрафиолетовый свет являются гауссовыми балками и распространены вдоль центра кристалла, интенсивность света является наиболее сильной в центре кристалла в процессе четырехлетнего четырехлета, а генерируемое тепло также является наиболее наибольшим. Следовательно, температура внутри кристалла распределяется в градиенте, а условия несоответствия фазы в каждом месте также различны. В настоящее время самая высокая эффективность преобразования может быть получена путем удовлетворения условия соответствия фазы в центре кристалла. Следовательно, под инъекцией зеленого света различных мощностей, полученных в эксперименте с четырехлетним четырехлетним, смещение температурыΔtустройства для нагрева кристаллического нагрева, когда достигается оптимальная мощность ультрафиолетовой выхода света, является тепло, генерируемым в центре кристалла, а распределение температуры в центре кристалла удовлетворяет:

В расчете этой статьи размер кристаллааВбеременныйоба 5 мм, радиус талии зеленого лучаω₀350 мкм, теплопроводностьkравно 1,4 Вт/(м · к), линейные коэффициенты поглощенияα₂₆₆иα₅₃₂кристалла для лазера 266 нм и лазера 532 нм оба 0,01 см^-1, поперечное сечение поглощения дефекта в цвете.σ= 8 × 10^-17см²и плотность центра цвета достигает устойчивого состояния при каждом значении, то есть времениТявляется ∞. Использование программного обеспечения для анализа конечных элементов в соответствии с уравнениями (9) до (13), нелинейный коэффициент поглощенияβ_Нлаи нормализованная плотность центра цвета при различных температурах сопоставления, которые влияют на генерацию кристаллического тепла, различные ультрафиолетовые лазерные мощности, могут быть теоретически решены. Результаты расчета показаны на рисунке 5.